数学月間の会
SGK通信2008-19(SGK懇話会資料)
数学月間懇話会(08/07/22)の資料をここにおきます:
1.数学月間(片瀬豊)⇒ KATASE_SGK.pdf
2.ある数学者たちの物語(上野正)⇒ UENO_Fermat001.pdf
3.数学と基礎科学(谷克彦)⇒ TANI_science.pdf
4.特別講演:秘法−数学的オブジェの照明(岡本和夫,河野俊丈)⇒ KOHNO_models.pdf
当日の写真アルバムのリンクは,SGK通信2008-13 の最下段にあります.
0
SGK通信2008-17(SGK懇話会によせて3)
竹内淳実氏にピタゴラス数の求め方を投稿していただきました.
−−−上野正氏の講演にもピタゴラス数の算出式がでてきました.
ここでは,竹内淳実氏が考えた簡潔な説明方法を紹介します.−−−
ここでは,竹内淳実氏が考えた簡潔な説明方法を紹介します.−−−
因数分解ができれば,簡単に理解でき,中高生の教材としての展開にも良いようです.
0
SGK通信2008-15(SGK懇話会によせて1)
SGK懇話会では質疑の時間がとれませんでしたが,
ご参加いただいた方々から,種々のコメントを戴いております.
”SGK懇話会によせて”として,順次掲載していきます.
このSGK通信も多くの方に読まれていることがわかりました.
ご意見,コメント何でもお寄せください.意見交換の輪を広げていきましょう.
SGK世話人:谷まで sgktani@gmail.com
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
★SGK懇話会によせて1
数学の重要性を誰もが認めるが,なかなか協力関係がなりたたないという話がありました。その理由には,一般の人々が数学を敬遠することもありますが,同時に,数学者が一般に向けて数学をわかりやすく説明することを怠っている(あるいは、わかりやすさに価値を認めない?)こともあると思います。(高木隆司氏)
高木隆司氏の最近の著書に,
「理科」「数学」が好きになる 楽しい数理実験
発行年月日:2008/06/20
サイズ:A5判 ページ数:190 ISBN:978-4-06-153137-6
定価(税込):2,520円
があります.私も興味深く読みましたが,内容は種々の形に関する実験を取り上げ,生徒にも明解にわかる本質をついた数学説明があります.
0
SGK通信2008-16(SGK懇話会によせて2)
数学月間に望みて,竹内淳実氏の詠みたる七言絶句(二題)「関孝和三百年忌」「聞米国数学月間有感」,および律詩(一題)「宇宙実験棟「希望」」,ここに掲載す.
関孝和三百年忌 平成二十年七月
元禄百花斎放殊 元禄百花斉しく放いて殊なり
算家互競遺題図 算家互いに競い題を遺んと図る
泰西学海未波及 泰西の学海未だ波及せざるに
何為関心相似乎 何為れぞ関心相似たる乎 (全部見るのはここ)⇒ 詠科学.pdf
0
SGK通信2008-13(数学月間懇話会報告)
第4回数学月間懇話会(14:00〜17:30)は,052教室で実施した.
片瀬豊,上野正,谷克彦,河野俊丈各氏により,4つの講演があった.
片瀬豊,上野正,谷克彦,河野俊丈各氏により,4つの講演があった.
講演資料は別途SGK通信に掲載予定です.
40人教室で懇話会を開始したが,50人を超す参加者があり,随時椅子を追加し10脚以上いれましたが収容スペースがない状態になりました.うれしい悲鳴ではありますが,教室後部の補助椅子の方々には,落ち着かない状況にしてしまいましたことをお詫びいたします.

数学的オブジェ見学(17:30〜18:00).岡本和夫(東大)氏により火入れ式が行われ,照明された3つの負定曲率曲面などの見学を行った.
18:00より,ルベソンベールに移動し,懇親会を行った.
(当日の写真はここをクリック)⇒http://picasaweb.google.co.jp/SGKtani/Photo_SGK
0
SGK通信2008-14(数学と生命科学−上智大学講演会の詳細)
講演会「数学と生命科学−数理モデルを中心として−」
SGK通信2008-9で紹介した講演会情報の詳細⇒上智大講演会詳細.pdf
これは日本数学協会「数学月間」参加プログラムです.
日時:2008年8月4日(月),13:30-17:00
場所:上智大学11号館411教室
場所:上智大学11号館411教室
・感染症対策における数理モデルの役割(大日康史)
・数理脳科学と情報幾何(甘利俊一)
世話人:金井寛(上智大学名誉教授),篠田健(上智大学理工学部教授)
0
SGK通信2008--12(数学月間懇話会-数学的オブジェ照明状況)
照明された”数学的オブジェ”
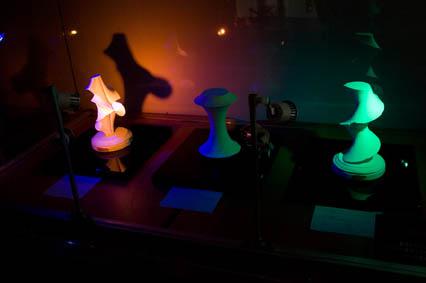 写真提供:飯村昭彦氏
写真提供:飯村昭彦氏(協力:東芝ライテック・ハリソン東芝・パール電球)
0
SGK通信2008-10(SGK懇話会)
−お知らせ−
以下の会合で,片瀬豊氏が「数学月間の話」をします.
日時:H20.7.19(土)12:30-14:00
場所:横浜クルーズ・クルーズ スカイビル27F
Tel:045-450-2111
主催:神奈川銀杏会・三士会
Tel:045-450-2111
主催:神奈川銀杏会・三士会
0
SGK通信2008-11(数学月間懇話会−数学的オブジェ写真)
東京大学大学院数理科学研究科所蔵の石膏幾何学模型は,19世紀末から20世紀初めにドイツで製作され,1910年代頃に輸入されたものである.今回,東芝ライテックなどの協力で,LED照明がなされた3点の模型は,いずれも負の定曲率曲面である.
(1) (2) (3)



(1) クエン曲面,負の定曲率曲面
ガウス曲率がいたるところ負の一定値をとる曲面の中で,最も複雑なパラメータ表示をもつものの一つである.曲面は自己交差をもつ形で3次元ユークリッド空間にはめこまれている.
(2) 回転面として得られる双曲面型の負の定曲率曲面
回転面として表される負の定曲率曲面には3通りのタイプがあることが知られていて,それぞれ,擬球,双曲型,円錐型とよばれている.この曲面は,その一つである双曲型の回転面である.
(3) ディニ曲面,負の定曲率の一般化されたヘリコイド曲面
トラクトリックスとよばれる曲線を回転すると負の定曲率曲面の典型的な例である擬球が得られるが,この曲面はトラクトリックスをらせんに沿って移動して得られるヘリコイド曲面である.
トラクトリックスとよばれる曲線を回転すると負の定曲率曲面の典型的な例である擬球が得られるが,この曲面はトラクトリックスをらせんに沿って移動して得られるヘリコイド曲面である.
-------解説:河野俊丈(東大)
0
SGK通信2008-9(講演会情報)
数学月間講演会の一つとして以下の講演会が計画されています.
「数学と生命科学−数理モデルを中心として−」(案)
日時:2008年8月4日(月):13:30-17:00
場所:上智大学
「数学と生命科学−数理モデルを中心として−」(案)
日時:2008年8月4日(月):13:30-17:00
場所:上智大学
プログラム(案)
13:30-15:00
講演者:大月康史氏(国立感染症研究所感染症情報センター)
題目:感染症と数学
15:30-17:00
講演者:甘利俊一氏(理化学研究所脳科学総合研究センター)
題目:数理脳科学と情報幾何
主催:上智大学理工学部数学科/情報理工学科
共催:上智大学理工学部/日本数学協会
世話人:金井寛(上智大学名誉教授),篠田健一(上智大学理工学部教授)
0

